これを10秒で答えられる人は数的感覚に優れているらしいｗｗｗｗｗ

1: 名無しカレッジ 2020/01/03 21:23:31 No.651918016 ▼このレスに返信

10秒で答えられる人は数的感覚に優れているらしい

2: 名無しカレッジ 2020/01/03 21:24:40 No.651918516 ▼このレスに返信

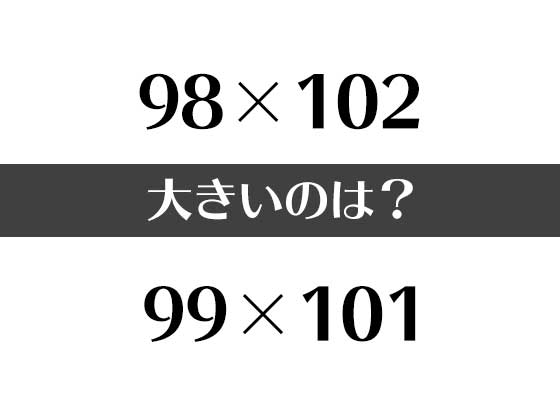
上はいっぱい！
下もいっぱい！
解なし！

4: 名無しカレッジ 2020/01/03 21:26:17 No.651919254 ▼このレスに返信

下が一瞬で分かるから上と比べるというゴリ押し方式

7: 名無しカレッジ 2020/01/03 21:28:00 No.651919982 ▼このレスに返信

98*2と99*1だとどっちが多いかみたいな数の省略をして考えられれば早く答えられるとか
そういう訓練的なやつ？

12: 名無しカレッジ 2020/01/03 21:30:29 No.651921030 ▼このレスに返信

>98*2と99*1だとどっちが多いかみたいな数の省略をして考えられれば早く答えられるとか
>そういう訓練的なやつ？
だいたい合ってる9800+196と9900+99の比較が出来ると早い

9: 名無しカレッジ 2020/01/03 21:29:31 No.651920598 ▼このレスに返信

数字を見ただけで諦めちまう歳になっちまったぜ

11: 名無しカレッジ 2020/01/03 21:30:23 No.651920981 ▼このレスに返信

98×101を基準に101と98のどっちが加算されると大きくなるか考えればいい

17: 名無しカレッジ 2020/01/03 21:33:05 No.651922114 ▼このレスに返信

いざ出されるとちょっと迷っちゃうな

20: 名無しカレッジ 2020/01/03 21:33:45 No.651922404 ▼このレスに返信

数的感覚も何もぱっと見て100と98なら100の方が大きいから下の方が大きいって分からない？

31: 名無しカレッジ 2020/01/03 21:37:55 No.651924201 ▼このレスに返信

>数的感覚も何もぱっと見て100と98なら100の方が大きいから下の方が大きいって分からない？
それが数的感覚なのでは…？

23: 名無しカレッジ 2020/01/03 21:34:35 No.651922778 ▼このレスに返信

掛けるほうが強いから上だろ

25: 名無しカレッジ 2020/01/03 21:36:48 No.651923759 ▼このレスに返信

一瞬で暗算できるん？

26: 名無しカレッジ 2020/01/03 21:37:03 No.651923862 ▼このレスに返信

どちらか大きいか答えるだけなら8*12と9*11で入れ替えて考えてみればいい

27: 名無しカレッジ 2020/01/03 21:37:12 No.651923921 ▼このレスに返信

極端に考えると 1×199 vs 100×100 になることにもっと早く気付きたかった

28: 名無しカレッジ 2020/01/03 21:37:43 No.651924126 ▼このレスに返信

8×2
●●●●●●●●
●○○○○○○○

6×4
●●●●●●
●○○○○○
●○○○○○
●○○○○○

白丸が錬金された面積

35: 名無しカレッジ 2020/01/03 21:39:34 No.651924847 ▼このレスに返信

>白丸が錬金された面積
言いたいことはわかるが錬金で駄目だった

30: 名無しカレッジ 2020/01/03 21:37:51 No.651924178 ▼このレスに返信

暗算で計算できるレベルじゃん

33: 名無しカレッジ 2020/01/03 21:38:56 No.651924591 ▼このレスに返信

こんなん知識というか経験則レベルでわかるよ…

34: 名無しカレッジ 2020/01/03 21:39:05 No.651924663 ▼このレスに返信

暗算で終わるのに数的感覚も何もないもんだ

37: 名無しカレッジ 2020/01/03 21:40:22 No.651925145 ▼このレスに返信

こんなことで喧嘩するのは理性が弱いってことでいいのかな

40: 名無しカレッジ 2020/01/03 21:41:08 No.651925449 ▼このレスに返信

>こんなことで喧嘩するのは理性が弱いってことでいいのかな
理性じゃなくて知性が弱いんでしょ

47: 名無しカレッジ 2020/01/03 21:48:07 No.651928379 ▼このレスに返信

(a+b)(a-b)=a^2-b^2
(100+1)(100-1)=10000-1
(100+2)(100-2)=10000-4

49: 名無しカレッジ 2020/01/03 21:49:14 No.651928861 ▼このレスに返信

100*98=9800+200-4=10000-4
100*99=9900+99=9999

54: 名無しカレッジ 2020/01/03 21:52:42 No.651930371 ▼このレスに返信

2秒の刹那でカリキュレーションは完了
あとは30年モノの赤ワインを数秒たしなんではい解答は上
QED終了

56: 名無しカレッジ 2020/01/03 21:54:22 No.651931117 ▼このレスに返信

>あとは30年モノの赤ワインを数秒たしなんではい解答は上
やべえメンタリストDaigoみたいでかっこいい…

62: 名無しカレッジ 2020/01/03 21:57:13 No.651932287 ▼このレスに返信

>あとは30年モノの赤ワインを数秒たしなんではい解答は上
間違ってるじゃねーか！

55: 名無しカレッジ 2020/01/03 21:52:57 No.651930474 ▼このレスに返信

うまく言えないけど200を二つに分けて分配する掛け算なら100×100が一番大きいんだから
そこに近い方が大きいって考え方だなあ
わざわざ計算してない

58: 名無しカレッジ 2020/01/03 21:55:54 No.651931737 ▼このレスに返信

>うまく言えないけど200を二つに分けて分配する掛け算なら100×100が一番大きいんだから
なるほど
俺まずそんな事も浮かばなかった…

66: 名無しカレッジ 2020/01/03 21:58:26 No.651932769 ▼このレスに返信

>うまく言えないけど200を二つに分けて分配する掛け算なら100×100が一番大きいんだから
>そこに近い方が大きいって考え方だなあ
チクショウこれが数学を感覚的に理解してるってやつなんだろうかねえ

70: 名無しカレッジ 2020/01/03 22:00:06 No.651933417 ▼このレスに返信

>うまく言えないけど200を二つに分けて分配する掛け算なら100×100が一番大きいんだから
>そこに近い方が大きいって考え方だなあ
>わざわざ計算してない
なんて分かりやすい解説なんだ…

60: 名無しカレッジ 2020/01/03 21:56:14 No.651931879 ▼このレスに返信

電卓を使う

61: 名無しカレッジ 2020/01/03 21:56:36 No.651932054 ▼このレスに返信

俺の方がデカい

共有: